孩子的开学综合症逐渐消退,进入了上学的常态。学有余力,便会生发出许多探究的触须。
昨日上午,一小三同学来hxy007家串门,这让007的孩子再次想起了两周前被老爸数学把戏整蛊的经历,缠着老爸要秘方。人家想学习,想探究,还不配合,这么当爹,那就太次了。007没办法,只好退让说:我可以和你们再来做一次游戏,但我不会告诉你们我的秘密。你们想知道的话,就自己做记录,自己去研究。
既然只做一次游戏,那就一次多试算几个数字。他们相互商量了一下,设计了一张表格,然后把自己设想的数字填上去。他们不让007看,但相互看了对方的表格一下,忍不住都哈哈大笑起来。看来,这两小鬼头要么用了特别大的数字,要么想出了特别怪的数字。007翻箱倒柜找出两个计算器,让他们在心算困难时使用。
游戏开始了,加1,乘3,加9,乘2,加27;个位、十位、百位……各个位数加起来,如果和还不是个位数,再各个位数加起来,一直加到加出一个个位数;用这个加出来的数乘以3,再加27。得数是50,对不对?
007在另一个房间里报出运算要求,根本看不到他们纸上写的东西,但不时地听到他们的议论——
他在使用混乱绝招。
这分明就是乘以9嘛!
这一步就可以开始凑了。
如果现在就要凑的话,我有三个可以。
我有一个不可以,没有破解,太好了!
检查一下。可恶,是我算错了,被他破解了!
结果出来了,看看儿子的记录吧。

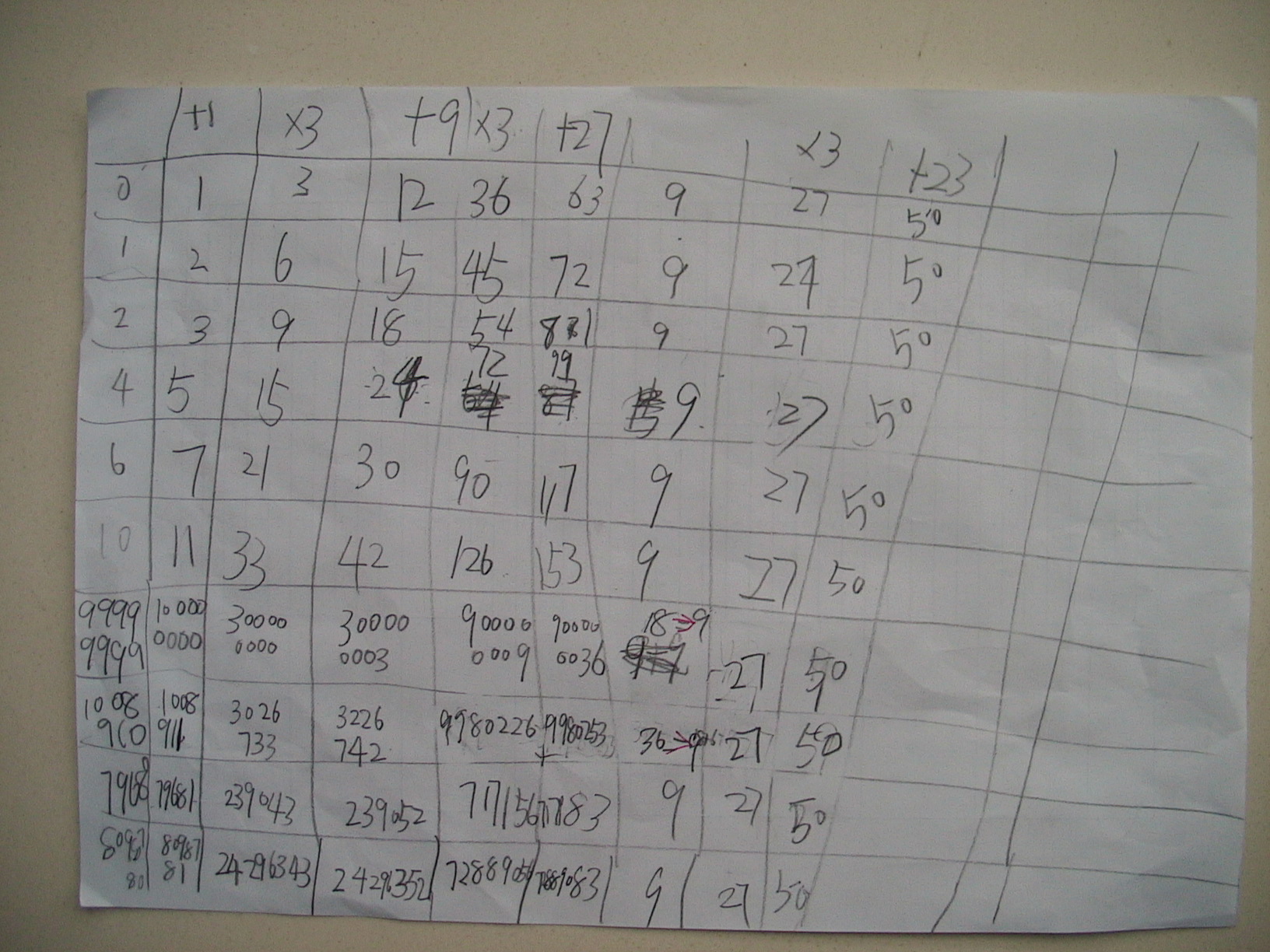
有份记录进行研究,方便多了!
很显然,无论前面如何运算,到了各位数相加时,最终的和一定是9。后面乘以3,加27,不过是障眼法而已。上次的游戏(见第25页1242楼),孩子们已经讨论过:什么样的两位数,其个位和十位相加会等于9?他们的结论是:18、27、36、45、54、63、72、81、90、99。他们还发现这些两位数有一些奇怪的特点:第一,它们都可以被9整除,是9的倍数;第二,这些数,个位与十位颠倒,还是9的倍数。现在,他们需要弄清楚的是:007老爹是怎么成功地使一个他不知道的数,经过一番运算之后,会变成这10个数中的一个呢?而实际上,他们运算下来的结果,有的时候并不是两位数,而是三位数甚至更大的数,这些数的各个位数加起来为什么会成为9的倍数呢?什么样的多位数,它们各个位数加起来会是9的倍数呢?
儿子把记录里这样的多位数统统找出来了,很快就发现记录里没有显示什么数其各个位数加起来会等于54、63、72、81。
007说:没有这样的数,难道你们不会编一个?你们想一想,什么数它们的各个位数加起来会等于54?随便想一个!
儿子说:六九五十四,999999,它的各个位数相加就是54.
小同学如法炮制:那9999999,它位的各个位数相加就是63.
007说:你们别偷懒,不用9,能不能想出个数,让它的各个位数相加等于72?
儿子说:九八七十二,888888888,它的各个位数相加就是72.
小同学也不是吃素的:88888888881,它的各个位数相加就是81.
呵呵,全齐了!——
9 ←117、153
9←18←99、900000036
9←27←717183
9←36←9980253
9←45←72889083
9←54←999999
9←63←9999999
9←72←888888888
9←81←88888888881
这些多位数有什么特点呢?
两个小三生开始琢磨起来,孩子他妈也加入进来了。首先,他们发现这些多位数,各个位数随便调换位置得出的新的多位数,各个位数加起来,还是9的倍数。这个自然是这样的,因为数字并没有换,只位置换了,这并不改变它们的总和。接着,他们提出猜想:这些多位数会不会像前面提到那10个两位数一样,也能被9整除,是9的倍数呢?
两个小三生立即分工,用计算器逐个进行检验。果如所料,它们都能够被9整除!只是最后一个数的检验,儿子的同学遇到了一个小麻烦。因为007提供的计算器只能显示10个数字,没法计算88888888881/9等于多少。只好手工计算啰?正要动手,被儿子制止。他说,因为他前面算过,888888888能够被9整除,所以88888888881也能被9整除。
007夫妻异口同声:为什么?
儿子笑了:前面那9个8可以整除的话,剩下的十位个位的81也会被9整除。它的商只要在后面加上0和9就行了!
妙哉!真的,007必须承认,自己也没有想到。
哈哈,007事先并不知道的那些数经过一番运算之后,都会变成9的倍数。可是,好像007并没有要求让这些数乘以9呀?这究竟是怎么回事呢?小同学已经没有耐心了,他觉得下次忽悠别人时,反正只要乘个9就得了。可是,儿子可能觉得被老爸忽悠了,还不明白一个所以然,有点冤,因此仔细地研究起整个运算过程来。

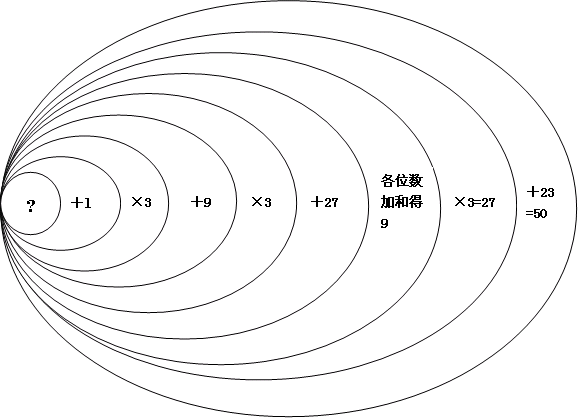
儿子琢磨了好一会儿,终于发现了老爸的狡猾。原来,第一步加1,是为了防止有人想的数是0,否则到后面做乘除时会一直是0;第二步乘3时,得数一定是3的倍数;第三步加9,得数还是3的倍数;第四步乘3,那就是9的倍数了;第五步加27,还是9的倍数;因此,到了第六步,所有9的倍数,各个位数相加,最终的得数肯定是9……
哈哈,原来如此。007蒙孩子,够狠的呀,几处使用障眼法!
儿子发现了这个秘密,非常兴奋,自己独自玩了好几盘。他的朋友回到家,当晚就把妈妈给整蛊了。今天上午,儿子也到院子里大耍把戏了。据他说,小朋友都被他整得特别崇拜他。不过,他玩过之后,产生了一个新的疑问。他告诉007,他试过别的数,比如5的倍数,各个位数相加不一定等于5;6的倍数也是这样。他问:为什么偏偏是9的倍数,它的各个位数加起来一定也是9的倍数,加到最后一定是9呢?
正等着儿子提出这个问题来呢!007心花怒放:这可不是玩了,这可是一个很有质量也很有趣的数学问题哟!人家Alex学弟对神秘的9颇有研究,早已经搞定了这个问题(见
http://ww123.net/baby/viewthread ... %3D1%26cycleid%3D52)。咱们不带急眼儿,不待急眼滴,蒿~~下次,咱们再找个时间,专门去请教。
儿子虽然还有疑问,但人家还是非常得意。他决定,明天到学校,就跟同学玩这个数学小魔术。但愿看到这个报告的明强BBMM能够体谅007家那小子,请别急于告诉你家孩子这个小把戏的秘密!最好也让孩子探索一番,一下子就知道“通项式”,就没有味道了。
未完待续……
[
本帖最后由 hxy007 于 2009-2-23 22:14 编辑 ].